hcapelo

M is for M-dwarf Models

by

When Prof. Brian Chaboyer visited from Dartmouth College, we heard all about theoretical models of M dwarfs – the smallest objects that are massive enough to properly be considered stars. Especially, he addressed the issue that for stars of about a half the mass of the Sun, current models predict main sequence stars that are either too luminous or too red by comparison to observations of stars in globular clusters. He explained that observational errors are down to about one percent, but that differences in theories vary by about four percent, and so the choice of model effects the interpretation of the observations. Whereas stellar atmospheric models can be verified by looking at the spectra of stars (Titanium Oxide is typically used to identify M-Dwarfs),  models of stellar interiors must map onto the bulk properties of the star such as radius, mass, age and rotation. To measure some of these bulk properties for comparison with his and other models, Prof. Brian Chaboyer studied transiting binary stars and compared his results to computational stellar structure models.

from http://www.sketchplease.com/index.php?s=matryoshka

Frenzied globs of gas though they may be, the interiors of stars can be dealt with by taking them to be spheres, composed of many concentric shells,  reminiscent of a Matryoshka doll.  One wants to know how four particular properties vary from the innermost shell to the outermost, such as pressure, mass, luminosity and temperature gradients. We expect these properties to be interdependent, and they are, which is reflected in four coupled differential equations of stellar structure. Using these equations is akin to asking the following questions:

 

Question: What change in pressure at each shell would be required to support a star against its own gravity?

Answer:

The Pressure is balanced by the force of gravity, defined in terms of the mass of each shell and the density.

 

Quenstion: How does the amount of mass differ between each shell?

Answer:

The total mass of the star can be arrived at by summing the mass density at every spherical shell.

 

Question: How much energy is passing through the surface of each shell at any given time?

Answer:

Luminosity is related to radius, density, and the rate of energy production by nuclear fusion or by changes in gravitational potential energy.

 

What is the temperature change at each layer?

…. This answer depends on whether energy transport occurs by radiation or convection.

For radiative heat transfer:

Derived by equating expressions for radiation pressure, the change in temperature relates to the opacity at a given shell, the energy flowing through it, and the temperature of the shell. By inspection, we can see that a high opacity and high luminosity give a steep temperature gradient, which is an impetus for convection. The opacities of small, cool stars are challenging because they are cool enough to contain molecules. There is another temperature gradient equation for convective transfer which comes from the first law of thermodynamics, and depends on which equation of state the gas can be considered to have. M-dwarfs are relatively compact stars where effects like degeneracy pressure play a role in the equation of state of the interior. (So said Prof. Pierre Demarque, Prof. Charboyer’s thesis advisor, who was in attendance at this colloquium.)

You can observe for yourself how some of the above properties change for stars of different mass using this applet made available by Dr. Brian Martin of King’s college.

Having a theoretical description of the bulk properties of the stars, Prof. Charboyer used a method employing binary star transits to find their radii. The basic idea was not unlike the now-familiar transit planet-finding method, in that measurements are taken during dips in the light curve when one of the orbiting bodies eclipses the other.

Image from ESA

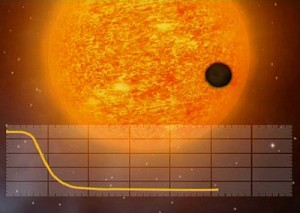
The transit planet-finding method gives the radius of a transiting companion relative to that of its companion. By contrast, Prof. Charboyer used the orbital velocity of the stars and the duration of the eclipse to establish the absolute radius of the objects. Taking the stars to be tidally locked – meaning that their rotational periods are given by their orbital periods – gives a rotation-radius relation that can then be used to fit to models. Prof. Charboyer reasoned that faster rotators would be stronger magnetic dynamos, causing them to have inflated radii, explaining the increased luminosity in observations. He didn’t consider such effects as differential rotation of the stars, but maybe we’ll hear more about that in relation to the Kepler mission targets if we receive a visit from Lucianne Walkowicz later this semester.

M-dwarfs themselves have come to be promising places to find habitable planets, precisely because the ratio of star to planet brightness is lower than for more massive stars. Thanks to the lower temperatures of M-dwarfs, habitable planets could exist close in to the star, their short periods making the chance of catching a transiting Earth-like planet pretty good.

 

 

 


 


 

 

 

Superluminosity: A Conversation in the Wake of Reported Faster-than-light Neutrinos.

by

A pair production between: Holly Capelo and Guy Geyer.


Holly: This fall was an exciting time to be studying special relativity, given that one of the most noteworthy recent science-news headlines was the possible violation of the universal speed limit, c, by superluminal neutrinos. Most of the press coverage on the OPERA report of a neutrino beam traveling through the Earth at a speed greater than light in a vacuum, was some variant on: “Einstein wrong, scientists baffled.” The attitude amongst most scientists I know was more like, “Let’s check the results, what a curiosity!” I myself wondered why Lorentz and Poincare’ weren’t given equal credit for the theory of special relativity.

As the process of investigating the results proceeds, we report on the most convincing evidence that there was no superluminal phenomenon detected, but first discuss what specifically was wrong with a paper that briefly offered the promise to explain the results using special relativity. Relativity can be counter-intuitive at times, so as a sanity check and to enrich the discussion, I have asked a fellow student, Guy Geyer to add his opinion on the same letter (which, according to Denis Overbye’s reporting, has been revised and is now under peer review, following the admission by the author of some of his early mistakes). Guy and I were asked to do a similar exercise at the culmination of a quarter-long course in Relativity taught by Prof. Fred Ellis this fall.

Since the Opera experiment released its results in September it has already received over 140 (and counting) citations from theories trying to justify the findings. Dr. van Elburg of the Department of Artificial Intelligence at the University of Groningen offered up a simple explanation for the recently-observed apparent superluminal motion of neutrinos passing through the Earth between an origin at Gran Sasso Italy to CERN Switzerland. He suggests that the measurement of the time of flight of the neutrino was actually measured from the frame of the GPS satellite, where length contraction would reduce the distance traveled according to the GPS clock, therefore shortening the time of required to cover the distance.
His paper was heavily reported upon, probably because it seems to be a simple solution that invokes special relativity and exactly reproduces the discrepancy in timing reported in the OPERA publication. This is attractive in some respects; after all, it is often a simple oversight that can disrupt a complicated process. Although, the solution may be a little too simple, since in order for special relativity to offer a sufficient explanation, one needs to establish that the Earth and satellite frames are inertial within the accuracy of the experiment – otherwise General Relativity must be invoked. As for the exact value of 64 nanoseconds, the striking similarity to the reported discrepancy may be accidental since the calculations made in the paper are done to very low-order precision.

Here are the elements of the experimental setup to consider:
The general procedure of measuring the neutrino flight time consist of a few procedural steps: 1. Determine the distance of the neutrino flight path baseline using a satellite – referred to as geodesy; 2. Bounce a radio signal originating from CERN off of a satellite towards the Gran Sasso location for the purpose of synchronizing cesium atomic clocks on either end (fiber optic cables running through the Earth were used to very verify the synchronization of the clocks and agreed to within 2 nanoseconds); 3. Having synchronized clocks at the neutrino production and detection sites, measure the distributions of departure and arrival times of the neutrinos in the Earth frame. The steps were carried out roughly in this order, although the geodesic measurements are on-going, as small shifts in the Earth’s crust need to be accounted for.

Guy: Regarding #2, This is the part of the experiment that I thought was most unclear… It isn’t really explained that well how exactly the OPERA clocks were synced. If they accounted for spec. and gen. relativity correctly to sync their clocks to earth frame time, then there shouldn’t be a problem. However, it’s still not clear to me that this is what is happening in their experiment.

Holly: You’re right, the original paper gives a schematic of these elements, but it isn’t entirely clear which calculations were made or how interdependent each of these aspects of the setup really are. Assuming that they are fairly independent, it seems to me that once the clocks are synchronized and the distance determined, then the satellite frame of reference becomes irrelevant to the measurement. Van Elburg defines a “foton” as a particle traveling at light speed, which could refer to either a radio photon used to synchronize clocks or to the neutrino beam itself. In failing to distinguish between these separate sets of events and paths in spacetime, he does not establish the need to consider the GPS frame when making the time measurement of the neutrino’s flight.
Van Elburg maintains that he is not concerned about a mistake in the time synchronization, but that the experiment could have been setup in the GPS clock frame.

Guy: I didn’t take away this impression – maybe there is something that I missed, but I thought he was saying that the mistake CERN made was that they didn’t properly account for how they were synchronizing the clocks.

Holly: Yes, I think that his argument boils down to a problem with the synchronization between clocks, but I ‘m not convinced that HE realizes that. I mean that Van Elburg claimed that the experiment was set up in the satellite frame and then proceeded to make some length contraction calculations of the baseline, but he doesn’t address any of the accompanying problems that come from trying to take coordinated time measurements between stationary and moving clocks. In particular, path- and velocity-dependent time dilation effects and a lack of synchronization with the Earth clocks would ensue.
I think the bottom line is that, although the details of the synchronization were not very explicit, Van Elburg’s premise that the experimenters forgot to change reference frames is easily refuted by looking to the original OPERA paper. The authors of the OPERA paper were conscious of having transformed back to the Earth Frame after measuring the baseline:

“The other fundamental ingredient for the neutrino velocity measurement is the knowledge of the distance between the point where the proton time-structure is measured at CERN and the origin of the underground OPERA detector reference frame at LNGS. The relative positions of the elements of the CNGS beam line are known with millimetre accuracy. When these coordinates are transformed into the global geodesy reference frame by relating them to external GPS benchmarks, they are known within 2 cm accuracy.”

So that would put the experiment back – at rest – on Earth once the baseline has been determined.

Guy and I weren’t the only ones to point out some ambiguities in the van Elburg paper which may have stemmed from the non-explicit nature of the OPERA paper itself. Such missing details make it difficult for outsiders (such as van Elburg or ourselves) to speculate about the experimental setup and any issues it may have had. Experimentally reproducing the results and proving the existence of physically related phenomena are likely to be more definitive tests of the claimed results.

More recently and perhaps more authoritatively, some relative insiders, involved with the sister project to the OPERA group known as ICARUS, have now produced a manuscript to be published in the Physical Review Letters verifying that none of the expected byproducts of superluminal motion were detected. Apart from the specific timing measurements, they considered by analogy one example where particles are known to travel faster than light speed in a given material**, which creates Cherenkov radiation. They argue that since neutrinos decay into additional particles as they lose energy, this energy loss both caps the maximum velocity of the particles and leads to the expectation that the decay products should have been detected. Using the same neutrino beam as the OPERA group, they found no such evidence for the expected decay behavior.

**Note that although the comparison to Cerenkov radiation is by analogy (the neutrino beam was claimed to have traveled faster than the vacuum speed of light) the fact that the particle beam did travel through a medium was lost on some people, leading to an embarrassing gaffe by the Italian Ministry of education, congratulating themselves for contributing to the construction of a “tunnel” between the two detector points (separated by over 500 KM, the longest tunnel in the world is about 20% this distance!) This statement received some cool response here. However, this is not the only tunnel that has been conjured in response to the findings, as dozens of theories evoking quantum behavior have arisen as well.

An Ultracool Colloquium

by

Each fall, the Astronomy department here at Wesleyan hosts a series of colloquia on a diverse set of topics in modern astrophysics. This is the first post reporting on these events. I’ll generally refer readers to the speakers’ websites for the details on their work, but will record interesting conversations that ensued when the speakers visited and give short informal primers on the research area under discussion.

The first colloquium speaker this fall was Dr. Trent Dupuy of the Harvard Smithsonian Center for Astrophysics. His talk was about “Testing Theory with Dynamical Masses and Orbits of Ultracool Binaries”.  As the title suggests, his work has focused on constraining evolutionary theories of brown dwarfs – intermediate objects that are often summarily described as either “failed stars” or the “missing link” between stars and planets. (For those who have memorized the stellar classification mnemonic, “Oh Be a Fine Guy/Gal Kiss Me”, they comprise additional “Lovingly Tonight Yes!” components of this imperative clause.)

Before the talk, we asked Dr. Dupuy if the current excitement about exoplanets has increased interest in his own work, given the similarities of brown dwarf atmospheres to planetary atmospheres. He answered yes. And no. In some sense analogies can be made, but much of the excitement that is driving the exoplanet searches is the possibility of finding terrestrial planets that could harbor life. Big gassy planets aren’t very relevant in that regard. Apart from their relationship to planets, brown dwarfs represent a rather unconstrained area within our current understanding of the lifetimes of stellar-type objects.  There is an excellent, accessible description of Dr. Dupuy’s thesis project here. Below I discuss some of the key characteristics of brown dwarfs.

Planets, brown dwarfs, and stars occupy a hierarchy based on their internal physics. Stars fuse hydrogen in equilibrium, brown dwarfs do not fuse hydrogen in equilibrium but do fuse deuterium for some portion of their evolution, and planets never fuse anything. Whether an object will fill one of these descriptions is determined by how massive it is. A star shines because of the thermonuclear reactions in its core, which release enormous amounts of energy by fusing hydrogen into helium. For the fusion reactions to occur, the temperature in the star’s core must reach at least three million Kelvin. Because core temperature rises with gravitational pressure, the star must have a minimum mass to provide this pressure. This is the so-called hydrogen burning mass limit, or HBML, as first defined and calculated by Kumar in 1963. Brown dwarfs have a mass less than the HBML which is about 75 times the mass of Jupiter. It was not until the mid-1990’s that the first brown dwarfs were directly detected, and so they are a relatively new field of study.

A robust signature of a brown dwarf is its total intrinsic brightness, or luminosity, but only at relatively late times in its lifespan. Just as there is a lower cut off in stellar mass, there is also a minimum luminosity for stars of around one ten-thousandth of the Sun’s luminosity. After a billion or so years, a star’s luminosity will become steady because of sustained nuclear fusion of hydrogen to helium in its core. Brown dwarfs don’t reach this steady condition, but “shine” by slowly cooling, thus gradually lowering their luminosity, eventually below the lower limit for a star. Luminosity is difficult to measure: the spectrum of the object has to be measured across a substantial portion of the electromagnetic spectrum and the astrometric distance to the object must be measured with good precision.

The temperature of a star can be inferred by the presence or absence of features in the stellar spectrum. For instance, the presence of methane is a signature of a cool brown dwarf. Methane can survive only at effective temperatures of less than 1500 Kelvin. By contrast the effective temperature of a star doesn’t drop below about 2000 Kelvin. It is actually the strong presence of methane in Gliese 229B -a much talked-about brown dwarf- that guaranteed that that object could not be a star. Gliese 229B orbits a red dwarf star, in a similar manner as a planet.

It is not uncommon for stars to orbit one another in binary systems. In fact most of what is understood about the relationship between mass and luminosity for typical stars is from the study of binaries. Orbiting bodies are well-described by Keplerian dynamics, in particular Kepler’s third law, which relates the period of an orbit, the mass of the objects and the distance between them. Dr. Dupuy is using the same fundamental procedure of studying brown dwarf binaries’ orbits and physical separations to determine their masses, and in turn constrain evolutionary theories about them. The fraction of binary systems comprised of brown dwarfs is relatively low, which provides a challenge to selecting suitable candidate systems to study.

Observationally, brown dwarfs are at the current limit of both infrared measurements and astrometry detections. Dr. Dupuy’s work has directly probed both of these limits by using laser adaptive optics at the Keck telescopes in Hawaii. While using some of the most advanced technology, he has taken a classical approach to measuring stellar masses by applying Kepler’s laws to binary systems. Observing stellar binaries enabled scientists of the late twentieth century to paint a very consistent stellar evolutionary picture. With improved brown dwarf mass determinations along with the wealth of new planetary data, this century will see the evolutionary details of the intermediate planet-star regime come into focus.

 

“…in this book as in The Hobbit the form DWARVES is used, although the dictionaries tell us that the plural of DWARF is DWARFS. It should be DWARROWS (or DWERROWS) if singular and plural had each gone its own way down the years, as have MAN and MEN, or GOOSE and GEESE.” J.R.R. Tolkien — Lord of the Rings – Appendix F-II