When Prof. Brian Chaboyer visited from Dartmouth College, we heard all about theoretical models of M dwarfs – the smallest objects that are massive enough to properly be considered stars. Especially, he addressed the issue that for stars of about a half the mass of the Sun, current models predict main sequence stars that are either too luminous or too red by comparison to observations of stars in globular clusters. He explained that observational errors are down to about one percent, but that differences in theories vary by about four percent, and so the choice of model effects the interpretation of the observations. Whereas stellar atmospheric models can be verified by looking at the spectra of stars (Titanium Oxide is typically used to identify M-Dwarfs), models of stellar interiors must map onto the bulk properties of the star such as radius, mass, age and rotation. To measure some of these bulk properties for comparison with his and other models, Prof. Brian Chaboyer studied transiting binary stars and compared his results to computational stellar structure models.
Frenzied globs of gas though they may be, the interiors of stars can be dealt with by taking them to be spheres, composed of many concentric shells, reminiscent of a Matryoshka doll. One wants to know how four particular properties vary from the innermost shell to the outermost, such as pressure, mass, luminosity and temperature gradients. We expect these properties to be interdependent, and they are, which is reflected in four coupled differential equations of stellar structure. Using these equations is akin to asking the following questions:
Question: What change in pressure at each shell would be required to support a star against its own gravity?
Answer:
The Pressure is balanced by the force of gravity, defined in terms of the mass of each shell and the density.
Quenstion: How does the amount of mass differ between each shell?
Answer:
The total mass of the star can be arrived at by summing the mass density at every spherical shell.
Question: How much energy is passing through the surface of each shell at any given time?
Answer:
Luminosity is related to radius, density, and the rate of energy production by nuclear fusion or by changes in gravitational potential energy.
What is the temperature change at each layer?
…. This answer depends on whether energy transport occurs by radiation or convection.
For radiative heat transfer:
Derived by equating expressions for radiation pressure, the change in temperature relates to the opacity at a given shell, the energy flowing through it, and the temperature of the shell. By inspection, we can see that a high opacity and high luminosity give a steep temperature gradient, which is an impetus for convection. The opacities of small, cool stars are challenging because they are cool enough to contain molecules. There is another temperature gradient equation for convective transfer which comes from the first law of thermodynamics, and depends on which equation of state the gas can be considered to have. M-dwarfs are relatively compact stars where effects like degeneracy pressure play a role in the equation of state of the interior. (So said Prof. Pierre Demarque, Prof. Charboyer’s thesis advisor, who was in attendance at this colloquium.)
You can observe for yourself how some of the above properties change for stars of different mass using this applet made available by Dr. Brian Martin of King’s college.
Having a theoretical description of the bulk properties of the stars, Prof. Charboyer used a method employing binary star transits to find their radii. The basic idea was not unlike the now-familiar transit planet-finding method, in that measurements are taken during dips in the light curve when one of the orbiting bodies eclipses the other.
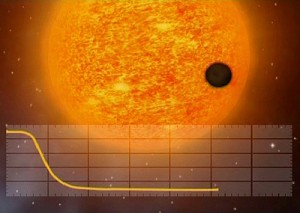
The transit planet-finding method gives the radius of a transiting companion relative to that of its companion. By contrast, Prof. Charboyer used the orbital velocity of the stars and the duration of the eclipse to establish the absolute radius of the objects. Taking the stars to be tidally locked – meaning that their rotational periods are given by their orbital periods – gives a rotation-radius relation that can then be used to fit to models. Prof. Charboyer reasoned that faster rotators would be stronger magnetic dynamos, causing them to have inflated radii, explaining the increased luminosity in observations. He didn’t consider such effects as differential rotation of the stars, but maybe we’ll hear more about that in relation to the Kepler mission targets if we receive a visit from Lucianne Walkowicz later this semester.
M-dwarfs themselves have come to be promising places to find habitable planets, precisely because the ratio of star to planet brightness is lower than for more massive stars. Thanks to the lower temperatures of M-dwarfs, habitable planets could exist close in to the star, their short periods making the chance of catching a transiting Earth-like planet pretty good.